Поиск в ширину
При поиске в ширину целевая вершина сначала отыскивается среди всех вершин, расположенных на данном уровне, прежде чем будут исследованы ветви, отходящие вниз от этих вершин (рис. 2.6). Иными словами, сначала ищем решение среди путей длины один, потом - длины два и т.д.
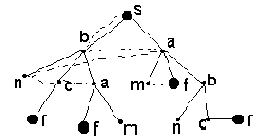 |
Рис. 2.6. Поиск в ширину
Очевидно, что этот поиск применим, даже если дерево бесконечно или практически бесконечно. К недостаткам этого поиска можно отнести неэффективность: если b - среднее число альтернатив для каждой внутренней вершины, то число путей длины n равно в среднем bn.
Поиск в ширину программируется на Прологе немного сложнее.
% поиск в ширину
solve(Start,Solve):-
width([[Start]],Solve).
width([[X|P]|_],[X|P]):- goal(X).
width(Ps,Solve):-
gener(Ps,Npath),
width(Npath,Solve).
newPath([],_,[]).
newPath([X|T],L,[[X|L]|LL]):-
newPath(T,L,LL).
postList(X,L,K):-
findall(Y, (next(X,Y),not member(Y,L)),K).
gener([[X|L]|T],Npath):-
postList(X,L,K),
newPath(K,[X|L],ZZ),
append(T,ZZ,Npath).
Предикат width(LL,S) использует аргумент LL для хранения всех начатых и еще не рассмотренных путей. LL представляет из себя список путей - список списков. Рассматриваемый в текущий момент путь является головой списка LL. Если этот путь приходит в целевую вершину, то решение найдено (это первое правило для width). Иначе применяется второе правило для width: создается новый список путей - кандидатов к рассмотрению - и рекурсивно вызывается снова width.
Предикат gener([[X|L]|T],Npath) удлиняет на одну вершину первый путь [X|L] из списка путей-кандидатов и множество удлиненных путей добавляется в конец списка путей-кандидатов. Используемый в нем вызов предиката postList(X,L,K) создает список K вершин-преемников вершины X, не принадлежащих списку L.
Проверим, как работает программа. Сначала поиск в ширину в графе на рис. 2.3:
?- solve(s,Solve).
Solve = [f, a, s] ;
Solve = [f, c, b, s] ;
Solve = [f, a, b, s] ;
Solve = [f, c, b, a, s] ;
No
Для задачи о кубиках поиск в ширину сразу выдает самое короткое решение:
?- run.
[[], [a, b, c], []]
[[], [b, c], [a]]
[[b], [a], [c]]
[[a, b], [c], []]
[[c, a, b], [], []]
Yes
Поиск в глубину и поиск в ширину относятся к стратегиям полного перебора. Эффективность поиска повышается, если упорядочить ветви, идущие от каждой вершины, - в первую очередь при переборе выбирать наиболее перспективные ветви. Мы используем это, скажем, при подъеме в гору, выбираем тропинки, идущие вверх. Другой пример: если вам надо на автомобиле пересечь незнакомый город в направлении с севера на юг, то вы предпочитаете ехать по широким улицам, идущим близко к этому направлению. Такая стратегия называется стратегией наискорейшего подъема (спуска).
Если мы отказываемся от полного перебора и отбрасываем некоторые, на наш взгляд, неперспективные ветви, то такой поиск называется эвристическим. Эвристический поиск быстрее находит решение, хотя и может быть неудачным. Пример: если мы должны выйти из леса в город, то следует предпочесть асфальтированные дороги проселочным.
