Поиск в глубину
Поиск в глубину основывается на следующей стратегии:
В каждой вершине выбирается какая-то определенная альтернатива, и ее изучение продолжается до тех пор, пока дальнейшее продвижение оказывается невозможным. Тогда процесс поиска возобновляется от ближайшей точки ветвления, имеющей неисследованные альтернативные варианты.
Поиск в глубину основывается на предположении "любой данный путь хорош, как и всякий другой". На рис. 2.5 показан порядок обхода вершин при поиске в глубину.
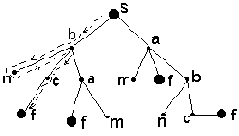 |
Рис. 2.5. Поиск в глубину
Поиск в глубину обладает следующими недостатками: а) во-первых, отыскивается не самый короткий путь; б) во-вторых, если в дереве есть бесконечные ветви и если такая бесконечная ветвь встретится - поиск никогда не закончится, даже если есть конечный путь в целевую вершину.
Поиск в глубину легко запрограммировать на Прологе.
% поиск в глубину
solve(Start,Solve):- % Start - начальная вершина, Solve - искомый путь
depth([],Start,Solve).
depth(P,X,[X|P]):-
goal(X). % этот предикат проверяет, является ли вершина целевой
depth(P,X,Solve):-
next(X,X1),
not(member(X1,P)),
depth([X|P],X1,Solve).
Предикат depth использует первый аргумент для накопления пройденного пути. Вершины в пути перечисляются в обратном порядке.
Для графа на рис. 2.3 мы можем экономно определить отношение next:
'ребра'([[s,b],[s,a],[b,n],[b,c],[c,f],[a,m],[a,f],[a,b]]).
next(X,Y):-
'ребра'(L),
(member([X,Y],L);member([Y,X],L)).
Добавим также к программе факт goal(f). Тогда имеем:
?- solve(s,X).
X = [f, c, b, s] ;
X = [f, a, b, s] ;
X = [f, a, s] ;
X = [f, c, b, a, s] ;
No
Вернемся к задаче о перестановке кубиков. Добавим предикат printList для удобной печати списка и предикат run для простоты запуска программы.
printList([]).
printList([H|T]):-
write(H),nl,
printList(T).
run:-
solve([[c,a,b],[],[]],Solve),
printList(Solve).
goal(S):- member([a,b,c],S).
Решим задачу:
?- run.
[[], [a, b, c], []]
[[a], [b, c], []]
[[b, a], [c], []]
[[], [c, b, a], []]
[[c], [b, a], []]
[[], [b, c], [a]]
[[b], [c], [a]]
[[], [c, b], [a]]
[[a], [c], [b]]
[[], [c, a], [b]]
[[c], [a], [b]]
[[], [a, c], [b]]
[[a], [b], [c]]
[[], [b, a], [c]]
[[b], [a], [c]]
[[], [c], [a, b]]
[[], [c], [a, b]]
[[c], [a, b], []]
[[a, c], [b], []]
[[], [b, a, c], []]
[[b], [a, c], []]
[[a, b], [c], []]
[[c, a, b], [], []]
Yes
У нас получилось поистине "ужасное" решение. Разберемся в чем причина. Во-первых, ситуации в найденном решении повторяются: например, состояния [[], [c], [b,a]], [[c], [b,a], []] и [[b,a], [c], []] в программе различаются. Это явилось следствием того, что в списке столбиков учитывается порядок. Для улучшения программы надо столбики рассматривать как элементы множества и заменить предикат member более сложным предикатом. Во-вторых, в решения встречаются два одинаковых состояния, идущих подряд
[[], [c], [a, b]]
[[], [c], [a, b]]
Это уже следствие недостаточно хорошего определения предиката next. Дело в том, что одним из состояний-преемников для [[], [c], [a, b]] является состояние [[c], [], [a, b]], которое предикат next выдает в виде [[], [c], [a, b]]. Здесь снова при программировании next надо учесть, что порядок перечисления столбиков в состоянии для нас не важен.
Если известна верхняя граница длины решающего пути, то можно ограничить глубину поиска.
% Поиск в глубину с ограничением глубины
solve(Start,Solve):- % Start - начальная вершина, Solve - искомый путь
depth([],Start,Solve).
depth(P,X,[X|P]):-
goal(X),
length([X|P],N),nl,
write('Нашли решение за '),write(N),write(' шагов '),nl.
depth(P,X,Solve):-
maxlength(Max),
length(P,N),
N+1<Max,
next(X,X1),
not(member(X1,P)),
depth([X|P],X1,Solve).
% maxlength(N) -> N - максимальная глубина;
maxlength(10).
Теперь, чтобы решить задачу (при поиске в глубину с ограничением 10) достаточно запустить цель
?- run.
Нашли решение за 10 шагов
[[], [a, b, c], []]
[[], [b, c], [a]]
[[b], [a], [c]]
[[], [c], [a, b]]
[[c], [a, b], []]
[[a, c], [b], []]
[[], [b, a, c], []]
[[b], [a, c], []]
[[a, b], [c], []]
[[c, a, b], [], []]
Yes
Поиск в глубину наиболее адекватен рекурсивному стилю программирования, принятому в Прологе. Причина этого состоит в том, что, обрабатывая цели, пролог-система сама просматривает альтернативы именно в глубину.
